O problema da satisfatibilidade booleana (SAT) [🇧🇷]
Na teoria da complexidade computacional, o problema da satisfatibilidade booleana (SAT) é reconhecidamente um dos primeiros NP-completo. O problema visa encontrar uma solução verdade para uma dada fórmula booleana, e caso encontrada, a fórmula é considerada “satisfatível”.
Por exemplo, se x1, x2, x3 e x4 são variáveis booleanas de uma fórmula booleana qualquer como:
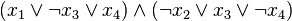
Caso seja possível encontrar valores para as quatro variáveis que torne a dada fórmula verdadeira, o problema SAT é resolvido.
Um problema do tipo SAT se torna mais simples quando é restringido a uma forma normal disjuntiva, onde todas as fórmulas lógicas são representadas por conjunções de cláusulas disjuntivas. Se torna mais simples ainda se o número de literais em cada cláusula for limitado por 2, passando a ser denominado 2-SAT problem (que pode ser resolvido em tempo polinomial).
2-SAT Problem
Um problema 2-SAT é representado por uma sentença lógica, composta de duas literais em cada cláusula, na forma normal disjuntiva como:
(a v b) ^ (~ c v d) ^ (e v f) ^ … onde a, b, c, d, … , são variáveis quaisquer que se pode atribuir valores verdade. Caso a sentença seja verdadeira para os valores atribuidos, o problema é satisfeito.
A primeira observação que temos é que (a v b) tem como equivalente a sentença (~a -> b v ~b -> a).
Se substituirmos todas as cláusulas disjuntivas pela sua equivalente do tipo “a implica b”, o problema 2-SAT pode ser modelado na forma de um grafo direcionado em que os vértices do grafo representam todas as literais e suas negações da sentença lógica (vértice ¬x sendo diferente de x) e as arestas representam as implicações das literais.
Exemplo (via wikipedia):
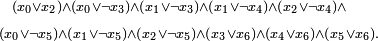
É modelado por:
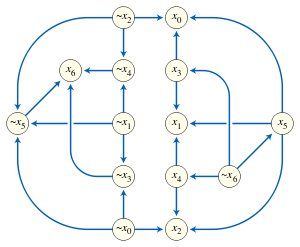
Sabendo que se qualquer condição encontrada do tipo “~a -> a” ou “a -> ~a” (ou seja, se existir caminho no grafo entre “a” e “~a”) nos daria uma sentença insatisfatível (prova) para qualquer valor atribuido às variáveis lógicas, o problema se resume a encontrar uma componente fortemente conexa, com Tarjan ou Kosaraju, e verificar se nessa componente conexa encontrada NÃO TEMOS as variáveis “a” e sua negação “~a”. Caso contrário, teríamos caminho entre uma literal e sua negação, invalidando a satisfatibilidade da sentença como explicado na prova contida no link acima.
Podemos descrever o algoritmo de resolução como:
1 - Modelar o grafo direcionado da sentença lógica;
2 - Encontrar componentes fortemente conexas;
3 - Verificar se alguma componente não contem uma literal e sua negação (dessa forma, não existindo caminho entre elas).
O cardápio da Sra. Montagny
- Problema: http://br.spoj.com/problems/CARDAPIO/
- Assunto Envolvido: Grafos, 2-SAT
- Linguagem Utilizada: C++
- Tempo de Execução: 0.61
- Uso de memória: 3.0M
- Nível: 7⁄10
Resumo do Problema
Sra Montagny quer realizar uma festa e verificar se é possível montar um cardápio que satisfaça ao menos um desejo de cada convidado da festa.
Cada convidado irá fazer 2 pedidos, contendo sua preferência de comida na festa, podendo ser uma das três hipóteses:
Duas comidas que ele gostaria de ver no cardápio;
Uma comida que gostaria e uma que não gostaria de ver no cardápio;
Duas que não gostaria de ver no cardápio.
Dicas para Resolução
Perceba que os pedidos dos convidados podem ser representados por uma sentença lógica na forma normal-disjuntiva em que cada cláusula disjuntiva represente os dois pedidos de cada convidado, de forma que precisamos verificar se existe alguma comida que se encaixe nessa sentença e possa torná-la satisfatível (caracterizando um 2-Sat Problem).
O problema se resume então em modelar o 2-Sat na forma de um grafo direcionado e verificar se alguma componente fortemente conexa desse grafo não contém qualquer literal e sua negação. Caso essa condição seja satisfeita, imprima “sim”. Caso contrário, imprima “não”.
Minha solução pode ser encontrada neste link.